Spectrum Profile and Shape Model

Introduction
Spectrum Systems Engineering (SSE) and TelePro, Inc., present a new rolling mill analysis and modeling software suite, the Spectrum Profile and Shape Model (SPS). This new product is an integrated package of proven mathematical models derived from the fundamental physics of the rolling process. These models are applicable to a wide variety of ferrous and non-ferrous, hot and cold flat rolling mills, accommodating both 4-high and 6-high roll stacks with roll bending and side-shifting variable crown work and/or intermediate rolls. Additionally, several commonly accepted mathematical models are included for the estimation of friction and material yield stress.
The software is structured to perform both process prediction and actuator preset calculations:
| Prediction Mode: | |
| Inputs: | Mill geometry, schedule parameters, and actuator settings. |
| Outputs: | Predicted rolling force, torque, extrusion, roll gap profile, and strip shape. |
| Preset Mode: | |
| Inputs: | Mill geometry, schedule parameters, and target exit strip shape or roll gap profile. |
| Outputs: | Required actuator settings for roll bending, roll side-shifting, and roll gap position. |
Sensitivities of roll gap profile and strip shape to changes in work roll bending and roll side-shifting are also calculated by the system. Knowledge of these sensitivities is essential for the design of on-line profile and flatness control systems.
A graphical forms-based user interface simplifies data entry, storage and retrieval of input data files, and viewing of results, including tabular and graphical display of model distributions and vectors.
Model Applications
The Spectrum Profile and Shape Model can be used in a variety of different environments for a variety of different applications:
Process Development and Optimization:
- Develop alternative rolling schedules.
- Investigate the effects of mill stack geometry changes (including roll diameters, crowns, and end relief) on contact force distributions, roll gap profile, and shape.
- Determine profile and shape actuator working ranges for specified rolling conditions.
Control System Development / Optimization:
- Calculate sensitivities of roll gap profile and strip shape to changes in actuator settings for profile and shape control.
- Calculate sensitivities of roll force, torque, and extrusion to changes in entry thickness, exit thickness, entry tension, exit tension, friction, and yield stress. These sensitivities are used in the design of non-interactive gauge and tension controls and for dynamic mill simulations.6
Off-line Mill Setup Calculations:
- Determine initial settings for roll gap position, work roll bending and work roll side shifting actuators for specified rolling conditions.
User Interface
The graphical user interface for the Spectrum Profile and Shape modeling suite is implemented using HTML web pages. This approach eliminates the need for the end user to purchase dedicated GUI software; instead, all that is required is a PC running a standard web browser. The use of web pages creates a platform independent user interface and assures that the graphics pages can continue to be supported even as new computing hardware and operating system software is introduced.
Input data for a given mill and schedule are entered manually into data entry forms located on a set of web pages. These pages allow the user to modify and configure all parameters applicable to the SPS model. Online help is available simply by clicking on any parameter name.
Different mill configurations and rolling schedules can be saved to and reloaded from files on disk.
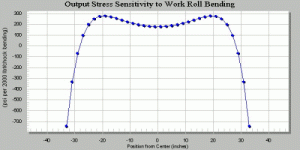
Model outputs may be viewed as text in tabular format or as graphical objects displayed in the web page. Below is an example of the plot of exit strip stress sensitivity to work roll bending.
Model Background
Roll Gap Model Fundamentals
The roll gap models calculate vertical rolling force, torque and extrusion ratio for hot and cold rolling of steel or aluminum strip and sheet. They can also be used in an adaptive mode, in which the predicted force is tuned to an experimental value by manipulation of the friction coefficient.
The theory is taken from published literature and is based on the widely accepted approach of Orowan.10 Enhancements to Orowan's work have mainly involved improved models of yield stress evolution and of friction between the strip and the work roll. Three extensions have been made to Orowan's basic structure for the Spectrum Profile and Shape Model. These include the Bland and Ford5 extensions to include the effects of elastic compression and recovery regions at entry and exit of the bite. Roll torque calculations developed by Alexander,1 and the modifications to them by Freshwater,7,8 have been added.
Three alternative models are included for estimating the friction between strip and work roll. These include the simple proportional Coulomb model as well as a "stick-slip" model with proportional friction limited by the strip yield stress in pure shear. Both of these approaches predict a sharp discontinuity in the friction stress at the neutral point - where the magnitude of the friction remains the same, but its direction reverses. This is physically unlikely and a number of models that characterize the frictional stress as dropping to zero near the neutral point have been proposed. The one described by Karabin and Smelser9 with a friction factor proportional to the relative surface speeds of the roll and the strip has been included.
It is generally agreed that the evolution of yield stress through the roll bite is a function of total strain, current strain rate and current temperature. For cold rolling, the yield stress is largely independent of strain rate (viscous effects) and temperature (which remains roughly constant), and a simple work hardening law relating yield stress to accumulated strain is used. For hot rolling, a "Sellars-Teggart" or "hyperbolic sine" relationship between effective strain rate and effective stress is most common in the literature and is used here.
Profile and Shape Model Fundamentals
The profile / flatness model describes the deformation of a 4-high or 6-high roll stack in response to a roll force distribution across the strip width. This roll force distribution can be specified as an input vector (stack-only mode), or can be computed by a strip deformation model (full flatness mode). The Spectrum Profile and Shape Model divides the roll stack into a number of discrete zones in the roll axis direction. It employs techniques proposed by Allwood and Bryant2,3 to reduce calculation time.
The profile/flatness model consists of a roll stack deflection model, roll deformation (squashing) model, and the roll gap model which are solved iteratively, subject to non-linear roll-to-roll contact conditions. The formulation used allows this nonlinear problem to be solved quickly. As a result, it is also feasible to use the model in the inverse or preset mode to compute shape actuator setpoints for a specified strip stress distribution.
Contact
If you have any interest in the Spectrum Profile and Shape Modeling Suite, please contact us.
References
1 Alexander J.M. (1972) "On the theory of rolling" Proc. R. Soc. Lond. A326 535.
2 Allwood J.M., Bryant G.F. and Stubbs. R.E. (1997) "An efficient treatment of binary non-linearities applied to elastic contact problems without friction", J.Eng Math, Vol 31 pp81-98.
3 Allwood J.M. and Bryant G.F. (1997) 'Fast modelling of roll stack behaviour for control applications', Proc. I. Mech. E. 211 373-386.
4 Allwood J.M. (1993) "On line modelling of shape phenomena in metal rolling", PhD Thesis, U. of London.
5 Bland D.R. and Ford H. (1952) "Cold rolling with strip tension Part III. An approximate treatment of the elastic compression of the strip in cold rolling" J. Iron Steel Inst. 171 245.
6 Bryant G.F., Edwards W.J. and McClure C.H. (1973) "Cold-rolling-mill control-system design" In "Automation of Tandem Mills" ed. Bryant G.F. The Iron and Steel Institute, London.
7 Freshwater I.J. (1996) "Simplified theories of flat rolling - I. The calculation of roll pressure, roll force and roll torque" Int. J. Mech. Sci. 38(6) 633-648.
8 Freshwater I.J. (1996) "Simplified theories of flat rolling - II. Comparison of calculated and experimental results" Int. J. Mech. Sci. 38(6) 649-660.
9 Karabin M.E. and Smelser R.E. (1990) "A quasi three-dimensional analysis of the deformation processing of sheets with applications" Int. J. Mech. Sci. 32(5) 375-389.
10 Orowan E. (1943) "The calculation of roll pressure in hot and cold flat rolling" Proc. I. Mech. E. 150 140-167.
11 Stubbs R.E. (1996) "Three dimensional behaviour of rolling mills", PhD Thesis, U. of London.
12 Timoshenko S. & Goodier J.N.(1951) "Theory of Elasticity", McGraw Hill Book Company, London.

